With continued miniaturization, the requirements for sub micron control of high bandwidth, high resolution, low inertia systems are becoming more and more stringent. To match this demand, the motion control industry has steadily moved to more powerful and higher resolution platforms. This iterative process has continued to drive improvements in the PID control loop and its capabilities from 8 bit systems in the 1980's to today's 16 to 32 bit architectures. Any control system however is only as capable as it's 'weakest' component. 20 bit encoders, 32 bit processors and 16 bit DACs are of limited benefit when the resolution of the amplifier is typically limited to only 12 bits. A 16 bit amplifier with the same high PWM frequency of a 12 bit allows for the full performance capabilities of a modern control system.
PWM Control
Servo amplifiers require a command signal from a motion controller which is then translated into a current supplied to a motor's coils. One of the most used amplifier types in servo control today is the PWM Amplifier or 'switcher.' Manipulation of motor current is achieved by quickly switching a series of power MOSFETs in an H Bridge configuration. During an interval defined by the PWM frequency (typically in the tens of KHz range), each coil is switched on and off. The ratio of how long the FET is on vs the total interval time is known as the duty cycle. The higher the duty cycle, the longer the FETs are on and the more current is delivered to the motor. Current resolution and responsiveness is then a function of two parameters, the switching frequency and the PWM duty cycle.
Figure 1: PWM Duty Cycle
Since the PWM duty cycle is controlled via a digital controller, it is by definition quantized or restricted to a range of discrete bits. For instance, a 12 bit PWM signal can assume one of 4096 discrete duty cycles. A 16 bit PWM signal provides 16 times the resolution of a 12 bit signal, providing 65,536 possible current values. If a servo amplifier is able to supply up to 10 Amps of current to a motor, the current resolution in a 16 bit PWM is 0.305 mA/bit as opposed to a 12 bit PWM signal which provides a current resolution of 4.88 mA/bit. Equation 1 dictates that the motor torque is also constrained to these values by the motor torque constant, KT. The end result is that higher resolution PWM control results in higher resolution torque control.
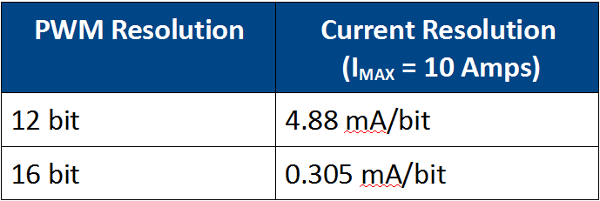
Table 1: Example current resolutions vs PWM resolution
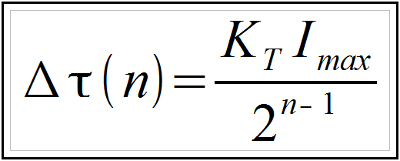
Equation 1: Relation of motor torque to current
Δτ(n): Torque resolution [Torque/bit]
n: PWM resolution [bits]
KT: Motor Torque Constant [Torque/A]
Imax: Amplifier maximum current rating [A]
Dead-band and Torque Ripple
The effects of PWM resolution are most evident when current demand falls between the discrete values set by the PWM signal. For the high resolution encoder system example shown in Figure 2 using a 12 bit PWM amplifier, as the position error increases from 0 to 15 counts no current is generated by the amplifier. Therefore there is no corrective torque to drive the system to eliminate the position error. This behavior effects the system in the same manner as a mechanical dead-band. With a 16 bit PWM amplifier even a single count of position error generates current from the amplifier eliminating the dead-band in the system.
Torque ripple is again the result of the PWM signal attempting to meet a current demand. In Figure 3, a current of 1.877 A has been commanded by the motion controller in order to move a mechanical system at a constant velocity. Assuming a +/-10 Amp range with a resolution of 12 bits, the amplifier can produce either 1.875 A or 1.8798 A. In order to achieve the desired current, the processor must modulate the command to be 1.8798 A for 1 sample and 1.875 A for 2 samples. The 16 bit amplifier can produce 1.8769 A or 1.8772 A and so as a result, the magnitude of the variation has been reduced by a factor of 16.
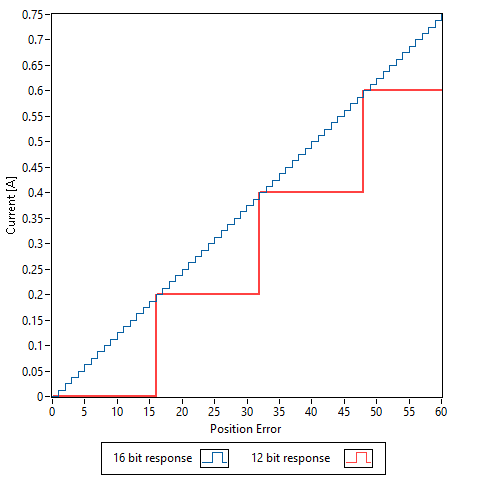
Figure 2: Torque response to position error
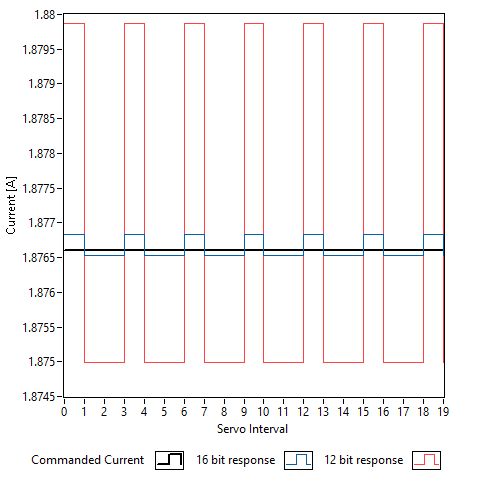
Figure 3: Effect of PWM resolution on torque ripple
The majority of mechanical systems possess enough inherent inertia and friction to make this ripple unnoticeable. Also for low to medium resolution systems, the dead-band effect of 12 bit amplifiers is not significant to prevent accurate control. In high resolution, low inertia, and high bandwidth systems however, the differences become more noticeable both in the system performance and production of undesirable audible noise. Linear or ceramic motors and low friction bearings are especially susceptible to these effects.
The Duty Cycle vs. Frequency Trade Off
Given that the advantages of a 16 bit PWM amplifier are clearly superior, why aren't all amplifiers made this way? The problem is maintaining a high PWM frequency. Typically a PWM frequency has an inverse relationship to the system clock frequency, as shown in Equation 2. For instance, with a system clock of 100 MHz a 12 bit PWM will have a frequency of 24.4 KHz (108/212). For a 16 bit PWM the frequency would be reduced to 1.5 KHz.
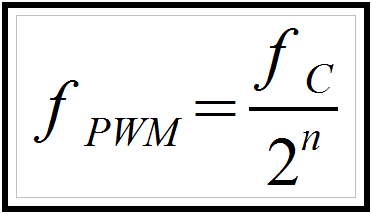
Equation 2: fPWM is the PWM frequency, fC is the system clock frequency, and n is PWM resolution
A PWM frequency this low has a number of drawbacks. First, it is well in the audible range and will no doubt be intolerable for any person within earshot. Second, the current bandwidth, which is a measure of how responsive the amplifier will be to commands, will be no better than one eighth of the PWM frequency. A bandwidth of 200 Hz is unacceptable in any high performance system. Finally the current ripple, which represents lost power and excess heat,
increases as the inverse square of the PWM frequency. Most sub-horsepower motors would burn up with a 1.5KHz frequency. The challenge then is to produce a 16 bit PWM amplifier to gain the benefits of high resolution while maintaining the high switching frequency necessary for a high performance practical control system.
A Fully Digital Drive
The Galil AMP-43540 Servo Amplifier has 16 bit PWM resolution while maintaining a PWM frequency of 33 kHz. The higher power AMP-43740 has 16 bits with a frequency of 20 kHz. Combined with sinusoidal commutation, these amplifiers provide high resolution torque control, high current bandwidth, fast response times, and minimal torque ripple in a fully digital drive. This capability makes these amplifiers the ideal solution for high performance control systems with low inertia, high resolution, or high bandwidth requirements.

